Chat

XY-Wing: Advanced Solving Sudoku Technique

XY-Wing by createclassicsudoku.com , and humage.com , and hodoku

XY-Wing:

XY-Wing is a method used to refine the candiates of a square with multiple candiates. Three empty squares are constrained in such a way that we can infer that some empty squares surely cannot be one certain number.

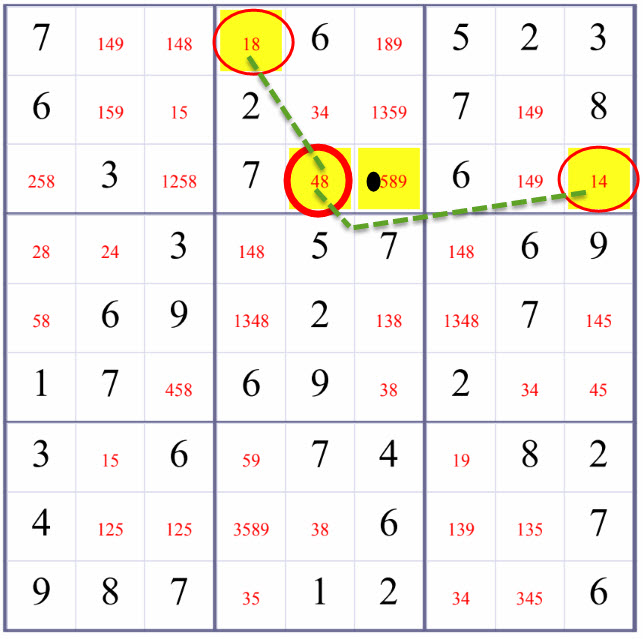
Below is an example of using XY-Wing-RowBox(one case of XY-Wing in our Sudoku solver, explained after the example) to refine the candidate values of R3C6 (the highlighted square that is not circled in red). Blank/Empty Squares are marked with candidate values in red.

For R3C5,

• if it takes number 4, R3C9 will have to take number 1;
• if it takes number 8, R1C4 will have to take number 1.

Either way, either R3C9 or R1C4 will be number 1.

Therefore, R3C6 who is at the same row as R3C9 and at the same box as R1C4 cannot be number 1. And we can safely remove number 1 from R3C6's candidate values.

These above two possibilites rule out the possiblity that number 1 could be in R3C6. We can safely remove number 1 from R3C6.

Hard Sudoku on 03/25/2018

Solve Hard Sudoku on 03/25/2018 in a step-by-step style

XY-Wing explained in a more detailed way:

When one square with candidates {X, Y} is in the same row, column, or box as a second square with candidates {X, Z};

This square is also in the same row, column, or box as a third square with candidates {Y, Z};

Candidate Z can be eliminated from the squares that is both at the same row, column, or box as the second square, and at the same row, column, or box as the third square.

For convenience, we call XY-Wing-RowBox, XY-Wing-ColBox, and XY-Wing-RowCol in our Sudoku solver.

XY-Wing-RowBox:

When one square with candidates {X, Y} is in the same row as a second square with candidates {X, Z};

This square is in the same box as a third square with candidates {Y, Z};

Candidate Z can be eliminated from the squares that is both at the same row, column, or box as the second square, and at the same row, column, or box as the third square.

XY-Wing-ColBox:

When one square with candidates {X, Y} is in the same column as a second square with candidates {X, Z};

This square is in the same box as a third square with candidates {Y, Z};

Candidate Z can be eliminated from the squares that is both at the same row, column, or box as the second square, and at the same row, column, or box as the third square.

XY-Wing-RowCol:

When one square with candidates {X, Y} is in the same row as a second square with candidates {X, Z};

This square is in the same column as a third square with candidates {Y, Z};

Candidate Z can be eliminated from the squares that is both at the same row, column, or box as the second square, and at the same row, column, or box as the third square.

How to find them?

• Use basic methods to solve the Sudoku until no further blank/empty square can be inferred to be a number using basic methods (Sole Candidate and Hidden Single).
• Write down the candidate values for every blank/empty square.
• Apply interaction methods, Subset, SubsetPosition, X-Wing methods if necessary.
• Check if one square with candidates X, Y is in the same row, column, or minigrid as two squares with candidates X, Z and Y, Z. If there exist such a blank/empty square, we can eliminate candidate Z from the squares in the same row, column, or minigrid as these two squares.