X-Wing: Advanced Solving Sudoku Technique
X-Wing by createclassicsudoku.com , and www.kristanix.com , and humage.com , and hodoku
X-Wing:
If in two rows all candidates of a certain digit are confined to two same columns, for these two columns this digit must appear within these two rows.
or
If in two columns all candidates of a certain digit are confined to two same rows, for these two rows this digit must appear within these two columns.
Candidate Numbers (or Candidate Values) of an blank/empty square is a list of 'possible values' or candidates for this blank/empty cell.
Take a look at these two possibilities of putting 5 in the fith row and the ninth row, aren't they form a Medium shape of 'X'?
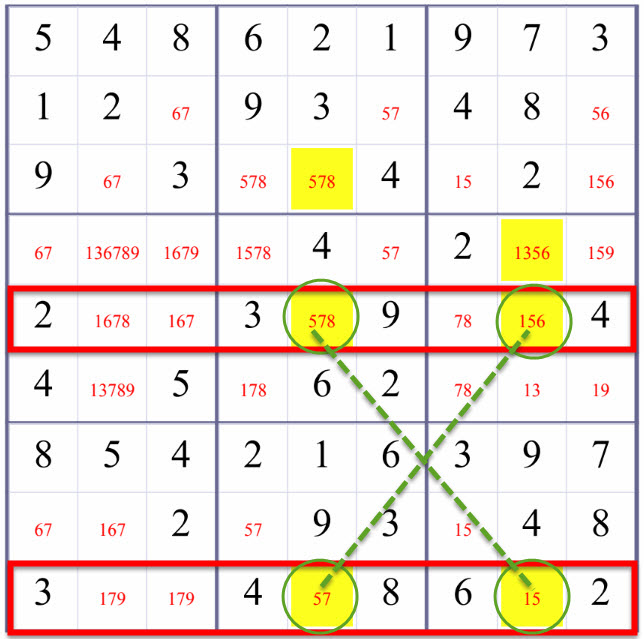
These above two possibilites rule out the possiblity that number 5 could be in R3C5 and R4C8 in the fifth column and the eighth column. Therefore, we remove number 5 from R3C5 and R4C8.
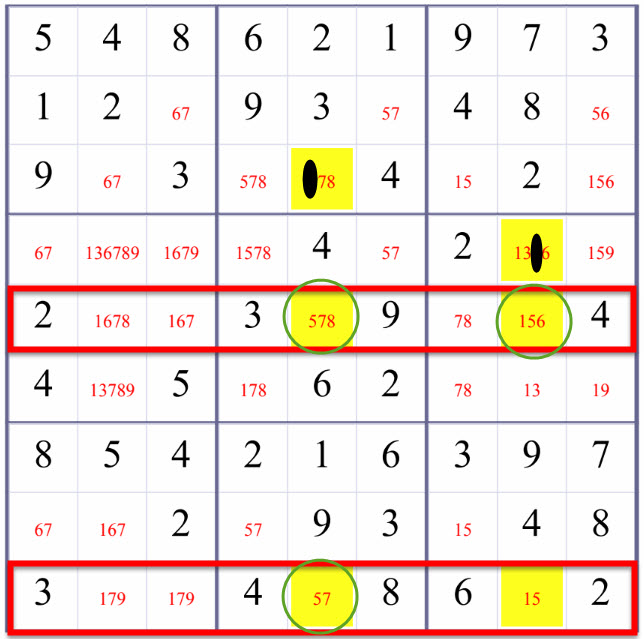
Solve Hard Sudoku on 03/22/2018 in a step-by-step style
Above is an example of using DoubleRowsOneDigitCheck(a.k.a. one case of X-Wing) to refine the candidate values of R9C9 (the highlighted squares in the fifth column and the eighth column excluding those at the fith row and the ninth row). Blank/Empty Squares are marked with candidate values in red.
In the fifth row and the ninth row, number 5 are confined to the fifth column and the eighth column. For the fifth row and the ninth row, let us check number 5.
- Either R5C5 and
R9C8 take number 5, or
- R5C8 and R9C5 take number 5.
For convenience, in our Sudoku solver, we call
DoubleRowsOneDigitCheck:
If in two rows all candidates of a certain digit are confined to two same columns, for these two columns this digit must appear within these two rows.
DoubleColsOneDigitCheck:
If in two columns all candidates of a certain digit are confined to two same rows, for these two rows this digit must appear within these two columns.
How to find them?
- Use basic methods to solve the Sudoku until no further blank/empty square can be inferred to be a number using basic methods (Sole Candidate and Hidden Single).
- Write down the candidate values for every blank/empty square.
- Apply interaction methods, Subset, SubsetPosition methods if necessary.
- Check if in two rows all candidates of a certain digit are confined to two same columns, for these two columns this digit must appear within these two rows. If there exist such a digit, remove this digit from candidate values of blank squares in that two columns but not in the two rows.
- Check if in two columns all candidates of a certain digit are confined to two same rows, for these two rows this digit must appear within these two columns. If there exist such a digit, remove this digit from candidate values of blank squares in that two rows but not in the two columns.